Parametrik Olmayan Testler -3

Kruskal- Wallis Testi

Daha önce parametrik olmayan testlere ilişin yayımlanan yazılara bakınız ( Parametrik olmayana testler-1 ve Parametrik olmayan testler -2 ).

İkiden fazla bağımsız grupta normal dağılım varsayımlarından en az biri sağlanamazsa veya örneklem sayısı yetersiz olduğunda ANOVA yerine Kruskal-Wallis Testi kullanılmaktadır.

Hiçbir varsayım olmadan Kruskal Wallis testi Tek Yönlü ANOVA testine alternatifi olarak tercih edilmektedir.

Kruskal Wallis testi için hipotezler şu şekilde kurulmaktadır:

H_{0 ;} µ₁ = µ₂   =… … … … =µ_k ( Gruplar arasında farklılık yoktur.)

H_{1 ;} µ₁ ≠ µ₂≠ … … … … ≠µ_k( Gruplar arasında farklılık vardır.)

Kruskal Wallis testi sonucunda H₀ hipotezi reddedilir ise bağımsız gruplar arasında fark vardır kararı verilir.

Farkın hangi gruptan kaynaklandığının belirlenmesi için ANOVA testinde olduğu gibi Çoklu Karşılaştırma testleri kullanılmaktadır. Farklılığın hangi gruptan kaynaklandığını belirlenmesi için Mann Whitney U testi yardımıyla ikili karşılaştırmalar yapılabilmektedir.

Ancak en az üç karşılaştırma yapılacağından yapılacak karşılaştırmada I. Tip Hata yapma olasılığı artacaktır. Bunun engellenmesi için  karşılaştırmalarda hata payı (α) karşılaştırma sayısına bölünerek belirlenmekte ve bu elde edilen hata payına göre karar verilmektedir.

Örnek: Parametrik varsayımların sağlanmadığı 3 farklı bölümde okuyan öğrencilerin 1. Vize sonuçları arasında farklılık olup olmadığının test edilmesi için gerekli adımlar aşağıdaki gibidir.

H_{0 ;} µ_İ = µ_E =µ_M ( Farklı bölümlerde okuyan öğrencilerin 1. Vize sonuçları arasında anlamlı bir farklılık yoktur.)

H_{1 ;} µ_İ ≠ µ_E ≠µ_M( Farklı bölümlerde okuyan öğrencilerin 1. Vize sonuçları arasında anlamlı bir farklılık vardır.)

Bu örnekte parametrik varsayımlar sağlanmadığı için aradaki farklılık Kruskal Wallis testi ile analiz edilebilir. Kruskal Wallis testi analizi için aşamalar aşağıdaki gibi sıralanmaktadır.

Örnek: 3 farklı bölümde okuyan öğrencilerin Vize sonuçları arasında farklılık olup olmadığının test edilmesi için gerekli adımlar aşağıdaki gibidir (Parametrik varsayımların sağlanamamaktadır):

H_{0 ;} µ_İ = µ_E =µ_M ( Farklı bölümlerde okuyan öğrencilerin Vize sonuçları arasında anlamlı bir farklılık yoktur.)

H_{1 ;} µ_İ ≠ µ_E ≠µ_M( Farklı bölümlerde okuyan öğrencilerin Vize sonuçları arasında anlamlı bir farklılık vardır.)

Bu örnekte parametrik varsayımlar sağlanmadığı için gruplar arası farklılığın test edilmesi için Kruskal Wallis testi kullanılmalıdır.

Kruskal Wallis testi analizi için aşamalar aşağıdaki gibi sıralanmaktadır.

Analyze/Nonparametric Tests/Legacy Dialogs/ K Independent Samples

Sekmeleri ardından açılan ekran aşağıdaki gibidir.

Ekranda, “Test Variable Test” kısmına bağımlı değişken, “Grouping Variable” kısmına bağımsız değişken aktarılır.

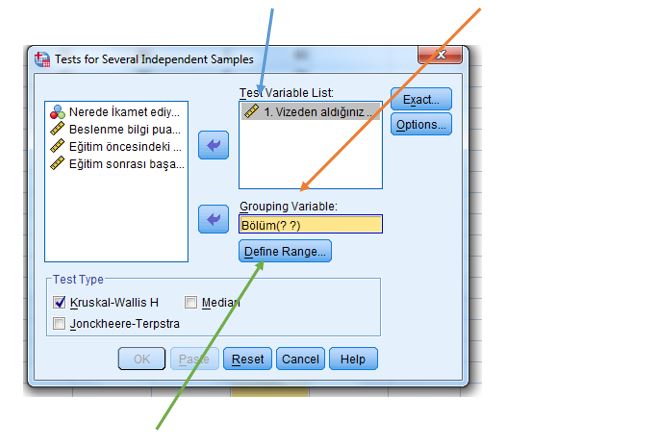
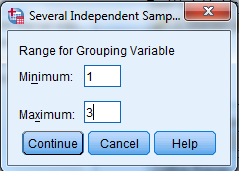
 “Define Range” sekmesi tıklanarak bağımsız değişkenin hangi kategorilerinin analize dahil edileceğinin belirlenmesi için bu değişkenin minimum ve maksimum değerleri girilir. Daha sonra “Continue” tıklanır:

Analiz sonucu elde edilen test çıktısı aşağıda yer almaktadır:

Ranks
	Bölümünüz?	N	Mean Rank
Vizeden aldığınız not?	İşletme	6	3,50
	Ekonomi	6	11,17
	Mimarlık	5	13,00
	Total	17

Test Statisticsa,b
	Vizeden aldığınız not?
Chi-Square	11,373
df	2
Asymp. Sig.	,003
a. Kruskal Wallis Test
b. Grouping Variable: Bölümünüz?

Test sonucu elde edilen ikinci tablo ise test istatistiklerini göstermektedir.

Sıra ortalamaları ele alındığında, “İşletme” bölümü öğrencilerinin sıra ortalamalarının diğer bölümlerden düşük olduğu görülmektedir. aldığı görülmektedir.

İkinci tabloda, p değeri 0.003 bulunduğu için H₀ ‘ i reddetmemiz gerekmektedir. Başka bir ifade ile, farklı bölümlerde okuyan öğrencilerin Vize sonuçları arasında istatistiksel olarak anlamlı bir farklılık olduğu söylenebilmektedir.

Bu farklılığın hangi bölümden kaynaklandığının belirlenmesi için ikili karşılaştırmalar yaparak karar verilmesi gerekmektedir.

Mann Whitney U testi, bağımsız değişkenin 2 durumunun test edilmesine olanak sağladığı için sırasıyla ikili karşılaştırmalar için kullanılmaktadır. İşletme ve Ekonomi bölümlerinin karşılaştırması için yapılan test sonucu elde edilen tablolar aşağıda yer almaktadır:

Ranks
	Bölümünüz?	N	Mean Rank	Sum of Ranks
Vizeden aldığınız not?	İşletme	6	3,50	21,00
	Ekonomi	6	9,50	57,00
	Total	12

Test Statisticsa
	Vizeden aldığınız not?
Mann-Whitney U	,000
Wilcoxon W	21,000
Z	-2,887
Asymp. Sig. (2-tailed)	,004
Exact Sig. [2*(1-tailed Sig.)]	,002b
a. Grouping Variable: Bölümünüz?
b. Not corrected for ties.

Burada hata payı I. Tip Hata yapma olasılığını azaltmak için 3 karşılaştırma söz konusu olduğundan 0.005/3 = 0.016 olarak ele alınmalıdır.

Bu örnekte elde edilen p değeri 0.004’tür. Bu değer 0.016’dan küçük olduğu için, İşletme ve Ekonomi bölümü öğrencilerin Vize notları arasında anlamlı bir farklılık olduğu söylenebilmektedir. Sırlama ortalamasına (Mean Rank) göre İşletme öğrencilerin Ekonomi öğrencilerine göre daha düşük not aldıkları sonucuna ulaşılabilir. Testin devamında diğer ikili karşılaştırmalar da aynı şekilde tekrarlanarak, farklılığın hangi bölümden kaynaklandığı belirlenmelidir.

Ki- Kare Testleri

Ki kare testleri süreksiz olayların testinde kullanılır. Parametrik olmayan testler arasında yer alan Ki kare testleri gözlenen ve beklenen frekanslar arasındaki farklılığın, anlamlı olup olmadığının incelenmesinde kullanılır. Ki kare testi analizden çapraz tablolardan yararlanılır. Ki kare testlerinde kullanılan çapraz tablolar 2X2 boyutlu olabileceği gibi çok boyutlu da olabilmektedir. Ancak çok boyutlu testlerde yeterli gözlem sayısına ulaşılmalıdır. Gözlem sayıları yeterli değil ise, düzeltme yapılmasına ihtiyaç vardır. 2X2 boyutlu Ki kare testi, 2 satır ve 2 sütundan oluşan bir çapraz tablodur. Bu boyutlu test için 4 gözlü Ki kare ifadesi de kullanılmaktadır.

Ki – kare testi uygulamanın amacı ve durumuna göre:

• Ki- Kare Bağımsız
• Ki-Kare Uygunluk (Uyum İyiliği)
• Ki-Kare Homojenlik, olmak üzere üç farklı Ki-kare testi vardır.

Ki –Kare Bağımsızlık Testi

İki değişken arasında bağımsızlığın olup olmadığını araştırmak amacı ile kullanılmaktadır.

Gözlenen frekanslar ile beklenen frekans değerleri birbirine yakınsa bağımsızlık olduğu söylenebilmektedir.

İki değişken arasındaki ilişkinin istatistiki olarak anlamlı olup olmadığını da ifade etmektedir.

Ki- Kare testinde sadece süreksiz veriler ( “Nominal” ve “Ordinal” ölçekler) kullanılabilir.

Ki- Kare için hipotezler:

H_{0 ;} Değişkenler birbirinden bağımsızdır (İlişki yoktur).

H_{1 ;} Değişkenler birbirinden bağımsız değildir (İlişki vardır).

Ki – Kare bağımsızlık testi istatistiğini kullanılarak karar verilebilmesi için Beklenen (frekansların) değerlerin 5’ten küçük olduğu hücre sayısının toplam hücre sayısının 20%’sini  aşmama şartı sağlanmalıdır.

Eğer 20%’i aşıyorsa ve gözlem sayısı arttırılamıyorsa, test sonuçlarına güvenilemez ve teste devam edilmemelidir. Bu durumda, ilgili satır ve sütunun mantıklı bir şekilde birleştirilmesiyle bu şart sağlananbilir ki SPSS’de bu işlem “Recode” komutu ile gerçekleştirilebilir. Ya da beklenen değeri 5’ten küçük olan hücreleri azaltmak için satır ve sütunun ilgili grupları analizden çıkarılabilir.

Bu iki seçenek çözüm için uygun değilse, test istatistiği kullanılamayacağından sadece çapraz tablo yorumlanabilir.

Örnek: Bireylerde varis oluşumunu fiziksel çalışma koşullarına göre incelemek isteyen bir hekim, elde ettiği verilere dayanarak ayakta ve oturarak çalışan bireylerde varis oluşumunun gözlenmesi ile gözlenmemesi durumlarının birbirinden bağımsız olup olmadığını incelemek istemektedir. Bu araştırmaya ait hipotezler aşağıdaki gibidir.

H_{0 ;} Bireylerin varis oluşumu ile çalışma şekli arasında bağımsızlık söz konusudur (ilişki yoktur).

H_{1 ;} Bireylerin varis oluşumu ile çalışma şekli arasında bağımsızlık söz konusu değildir(ilişki vardır).

Bağımsız Ki-kare testi için izlenecek yol aşağıdaki gibidir:

Analyze / Descriptive Statistics/ Cross Tabs

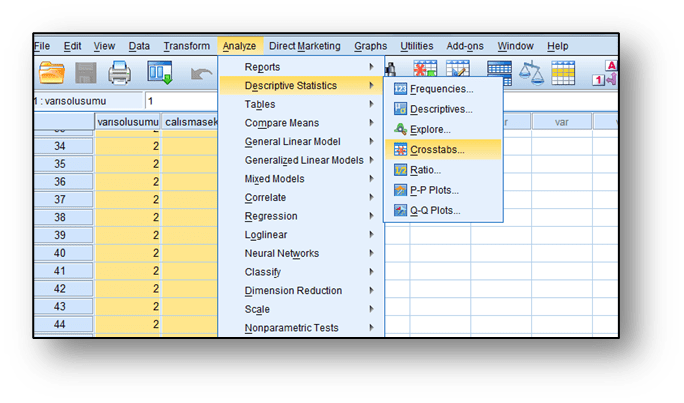
Seçeneği tıklandığında aşağıdaki ekran elde edilmektedir.  Bu ekranda daha önce çapraz tablo oluşturmada bahsettiğimiz gibi değişkenlerin aktarılmasından sonra “Statistics” sekmesi tıklanır. Açılan ekrana “Chi-square” seçeneği işaretlenir ve “Continue” tıklanır:

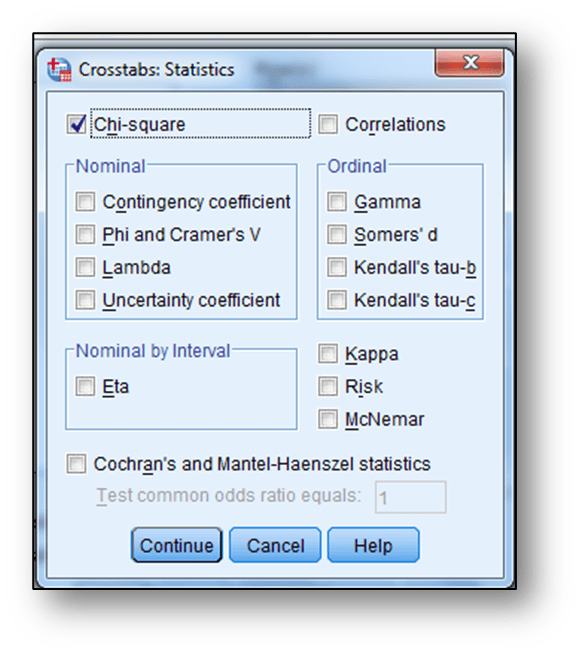
Daha sonra “Cells” sekmesi tıklanarak aşağıdaki işaretlemeler yapılır ve önce “Continue” sonra “OK” butonlarına tıklanarak analiz sonlandırılır.

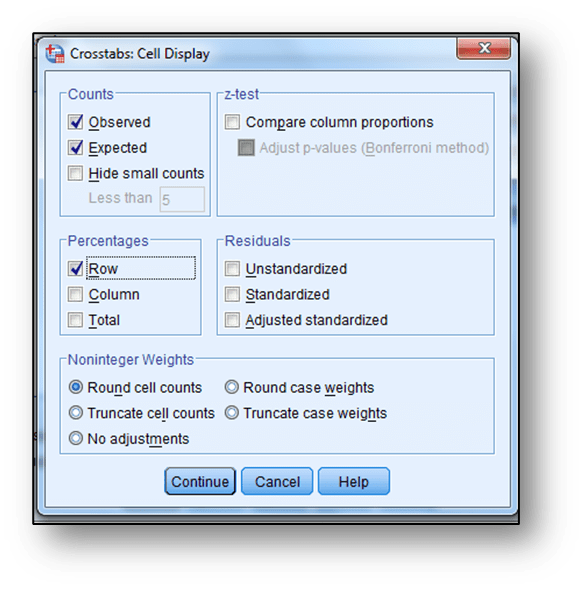
Analiz sonucunda çıktı olarak elde edilen tablolar aşağıdaki gibidir:

İlk tablo veri ile genel bilgiler sağlamaktadır. Bu örnekte toplam 50 veri olduğu ve kayıp veri olmadığı görülmektedir.

Case Processing Summary
	Cases
	Valid		Missing		Total
	N	Percent	N	Percent	N	Percent
varisolusumu * calismasekli	50	100,0%	0	0,0%	50	100,0%

İkinci tablo çapraz tablo olup hem gözlenen frekans hem de beklenen (expected) frekansları vermektedir. Bu örnekte varisi olup ayakta çalışan 20 kişi vardır, beklenen frekansı ise 16,2’dir.

varisolusumu * calismasekli Crosstabulation
			calismasekli		Total
			ayakta	oturarak
varisolusumu	yok	Count	7	13	20
		Expected Count	10,8	9,2	20,0
		% within varisolusumu	35,0%	65,0%	100,0%
	var	Count	20	10	30
		Expected Count	16,2	13,8	30,0
		% within varisolusumu	66,7%	33,3%	100,0%
Total		Count	27	23	50
		Expected Count	27,0	23,0	50,0
		% within varisolusumu	54,0%	46,0%	100,0%

Son tablo ise Ki-kare bağımsızlık test istatistiklerinin yer aldığı sonuç tablosu olup altında yer alan bilgiler önem arz etmektedir. Burada 5’ten küçük beklenen frekansların hücrelerdeki yüzdesi verilmektedir ve eğer beklenen frekansların %20 veya daha fazlası 5’ten küçük ise “Fisher Exact Test” satırına göre hipotezler test edilmelidir. Bu örnekte bu tür bir durum söz konusu değildir. Minumum beklenen değer 9.20 olarak bulunmuştur.

Chi-Square Tests
	Value	df	Asymp. Sig. (2-sided)	Exact Sig. (2-sided)	Exact Sig. (1-sided)
Pearson Chi-Square	4,844a	1	,028
Continuity Correctionb	3,653	1	,056
Likelihood Ratio	4,906	1	,027
Fisher’s Exact Test				,043	,028
Linear-by-Linear Association	4,747	1	,029
N of Valid Cases	50
a. 0 cells (0,0%) have expected count less than 5. The minimum expected count is 9,20.
b. Computed only for a 2×2 table

Örneğimizde hücre frekans değerleri ile ilgili herhangi bir sorun olmadığı için analizde Pearson Chi-square testi sonucu kullanılır. Örnekte p değeri 0.028 olarak bulunmuştur. Bu sonuca göre (p<0.05) H₀ hipotezi reddedilmelidir. Bu durumda “Çalışma şekline göre varis oluşumu arasında anlamlı bir fark vardır veya bağımsızlık söz konusu değildir” ve ” Varis oluşumu çalışma şekline göre değişiklik göstermektedir.” şeklinde yorumlanır.

Ki –Kare Homojenlik Testi

İki ya da daha fazla bağımsız örneğin aynı kategori açısından homojen olup olmadığına, yani bu bağımsız örneklerin aynı anakütleden seçilip seçilmediğini incelemek için kullanılır. Bu test için hipotezler şu şekildedir:

H_{0 ;} Örnekler aynı kültleden seçilmiştir. (Homojenlik vardır.)

H_{1 ;} Örnekler aynı kütleden seçilmemiştir. (Homejenlik yoktur.)

Örnek: A ve B olmak üzere iki ayrı şekilde üretilen aynı ürünün aynı kalitede olup olmadığını gösteren veriler ile Ki-kare homejenlik testi ile analiz edilir ve hipotezler aşağıdaki şekilde kurulur:

H_{0 ;} Örnekler aynı kültleden seçilmiştir (Homojenlik vardır).

H_{1 ;} Örnekler aynı kütleden seçilmemiştir (Homejenlik yoktur).

Ki – kare homojenlik testinde ki- kare bağımsızlık testinde olduğu gibi değişkenlerin frekanslara göre ağırlıklandırılması gerekmektedir. Analizden önce bu ağırlıklandırma işlemi yapılmalıdır. Bu işlemi gerçekleştirmek için

Data / Weight Case

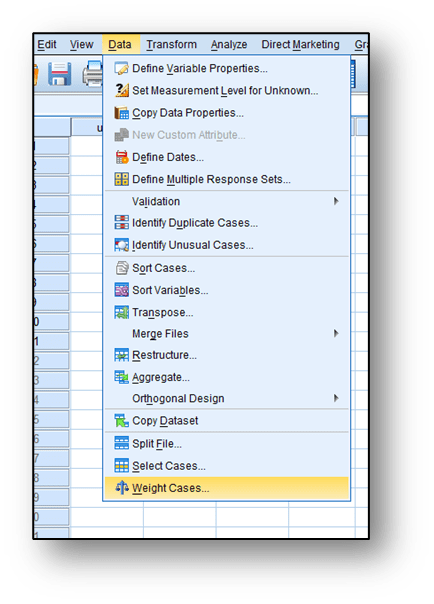
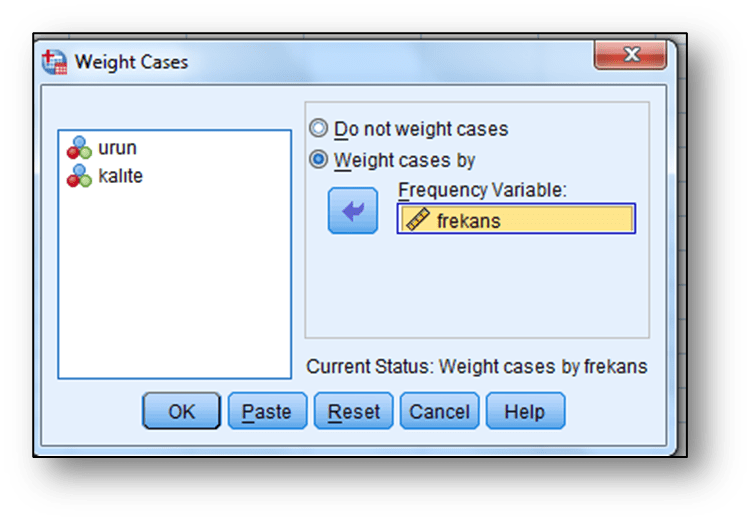
Sekmelerine tıklanması ile açılan ekrana “Weight case by” seçeneği işaretlenir ve bu seçeneğin altında yer alan ekrana frekans olarak tanımlanan frekans değişkeni aktarılır ve “OK “ tıklanır.

Bu işlemin ardından analiz için;

Analyze / Descriptive Statistics/ Cross Tabs

sekmelerinden çapraz tablo ekranı açılır. Burada çapraz tablo oluşturma işlemleri tekrarlanır:

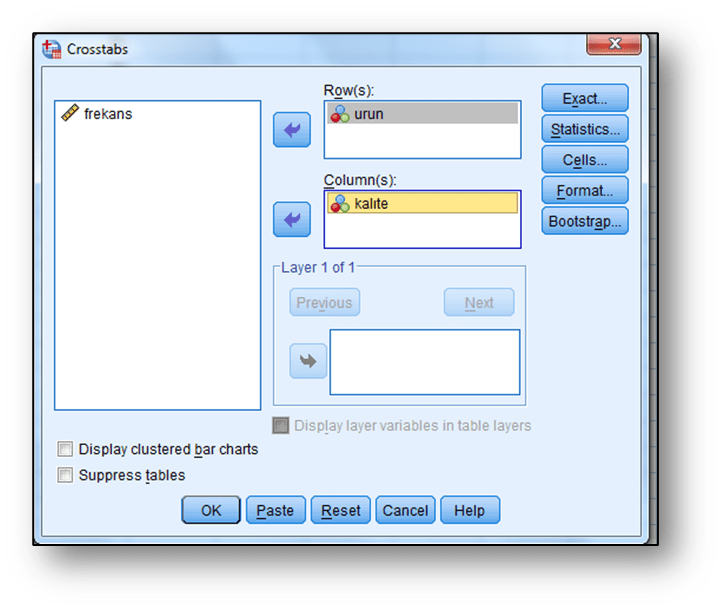
Çapraz tablo oluşturma işleminden farklı olarak “Statistics” sekmesinden “Chi-square” istatistiği işaretlenir ve “Continue” tıklanır.

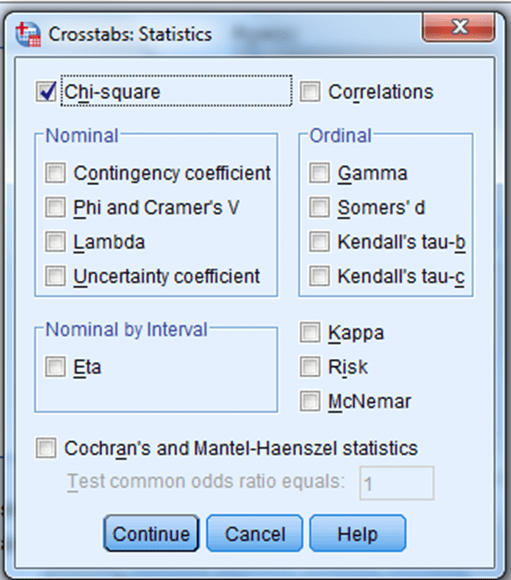
Sonra “Cells” sekmesi tıklanır, açılan ekranda gözlenen ve beklenen frekanslar için  “Observed” ve “Expected” seçenekleri işaretlenir, önce “Continue” ve daha sonra “OK” tıklanarak analiz sonuçlandırılır:

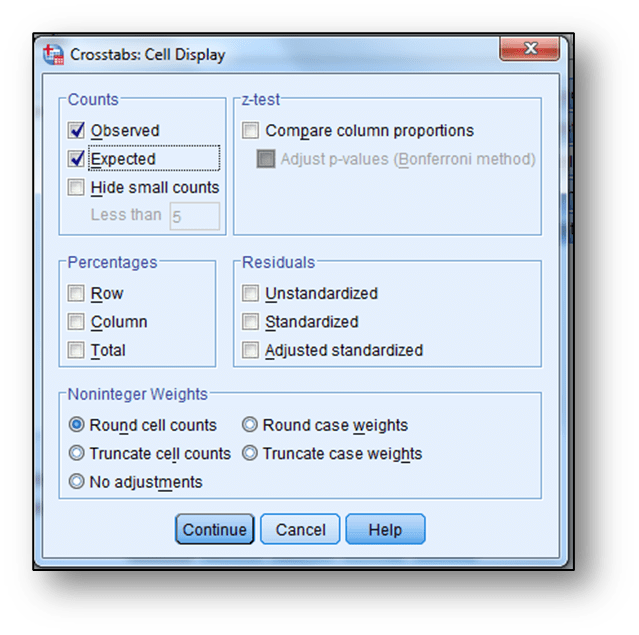
Analiz sonucu elde edilen IBM SPSS çıktıları aşağıda yer almaktadır:

Case Processing Summary
	Cases
	Valid		Missing		Total
	N	Percent	N	Percent	N	Percent
urun * kalıte	270	100,0%	0	0,0%	270	100,0%

urun * kalıte Crosstabulation
			kalıte		Total
			kalıtelı	kalıtesız
urun	a	Count	37	150	187
		Expected Count	68,6	118,4	187,0
	b	Count	62	21	83
		Expected Count	30,4	52,6	83,0
Total		Count	99	171	270
		Expected Count	99,0	171,0	270,0

Chi-Square Tests
	Value	df	Asymp. Sig. (2-sided)	Exact Sig. (2-sided)	Exact Sig. (1-sided)
Pearson Chi-Square	74,644a	1	,000
Continuity Correctionb	72,299	1	,000
Likelihood Ratio	74,936	1	,000
Fisher’s Exact Test				,000	,000
Linear-by-Linear Association	74,368	1	,000
N of Valid Cases	270
a. 0 cells (0,0%) have expected count less than 5. The minimum expected count is 30,43.
b. Computed only for a 2×2 table

Ki- Kare testi sonucu p değeri 0.000 olarak bulunmuştur. Bu durumda H₀ hipotezi reddedilir: Örneklerin aynı ana kütleden seçilmediği yani homojen olmadığı söylenebilmektedir.

Ki- Kare Uygunluk Testi

Belirli bir değişkenin farklı kategorileri için gözlenen frekanslarının, beklenen frekanslara uygunluğunu incelemek için kullanılmaktadır. Başka bir ifade ile, beklenen frekanslara göre hesaplanan dağılımın, gözlenen frekanslara göre hesaplanan dağılıma uygun olup olmadığı incelenmektedir. Bu nedenle Ki-kare uygunluk testi olarak adlandırılmaktadır ve hipotezler aşağıdaki şekilde kurulmaktadır:

H_{0 ;} Uygunluk vardır.

H_{1 ;} Uygunluk yoktur.

Bu teste Ki-kare bağımsızlık testinden farklı olarak serbestlik derecesine dikkat edilmelidir.

Örnek: İki farklı şekilde üretilen A ve B ürünlerinin eşit oranda üretilip üretilmediğini incelemek için;

H_{0 ;} A ve B ürünleri eşit oranda üretilmektedir (dağılım tekdüzedir).

H_{1 ;} A ve B ürünleri eşit oranda üretilmemektedir (dağılım tekdüze değildir).

 Hipotezi test etmek için IBM SPSS üzerinden izlenecek adımlar aşağıda yer almaktadır:

Analyze / Nonparametric Tests /Leagacy dialogs/ Chi Square

Sekmelerine tıklanarak açılan ekranda “Test variable list” alanına test edilecek değişken aktarılır ve kurulan hipotezin durumuna göre “Expected values” seçeneğinde gerekli düzeltmeler yapılır. Burada eğer temel hipotez değişkenlerin düzeyinde eşitliği ifade ediyorsa “All categories equal” seçeneği tıklanır. Eğer temel hipotez farklı oranlar üzerinde kurulduysa burada “Values” seçeneği tıklanarak ilgili oranların yazılması gerekir.

Bu işlemden sonra “OK” butonuna tıklanır ve IBM SPSS çıktı ekranında aşağıda yer alan tablolar elde edilir:

urun
	Observed N	Expected N	Residual
a	187	135,0	52,0
b	83	135,0	-52,0
Total	270

Elde edilen birincii tabloda gözlenen ve beklenen frekans bilgileri ve beklenen ile gözlenen frekansların arasındaki fark verilmektedir.

Bu örnekte A ürününden 187 tane vardır. Bu üründe beklenen değer 135’dir. Bir diğer değişle A ürünü beklenenden 52 tane fazladır.

Test Statistics
	urun
Chi-Square	40,059a
df	1
Asymp. Sig.	,000
a. 0 cells (0,0%) have expected frequencies less than 5. The minimum expected cell frequency is 135,0.

İkinci tabloda ise p değeri 0.000 olarak bulunmuş ve 0.05’ten küçüktür. Bu nedenle H₀ hipotezini reddedilmesi gerekmektedir. Diğer bir değişle iki farklı türde üretilen A ve B ürünleri eşit oranlarda üretilmemektedir.

Güvenilirlik ve Geçerlilik: (Cronbach α Katsayısı)

Genellikle araştırmalarda çok sayıda sorudan oluşan ve belirli bir amaca yönelik ölçüm yapmak için çeşitli ölçekler geliştirilmektedir. Ölçme ile elde edilen sonuçların farklı ölçümler sonucunda aynı olması, sonuçların güvenilirliğinin ve sonuçların tesadüfi olmadığının göstergesidir. Güvenilirlik, bilimsel araştırmaların en önemli şartlarından ilkidir.

Güvenirliliğin düşük olması, yapılan çalışmaların değersiz olduğunu ifade etmektedir. Güvenirlik göstergesi olarak güvenilirlik katsayısı hesaplanmakta ve değeri 0 ile 1 arasında değişmektedir.

Güvenirlik katsayısı hesaplanırken en çok kullanılan yöntem “Cronbach α Katsayısı”dır.

Cronbach α Katsayısı 0 ile 1 arasında bir değer alır. Eğer bu α değeri;

0 ≤ α < 0.5 ise güvenilir değil

0.5 ≤ α < 0.6 ise düşük güvenilir

0.6 ≤ α < 0.7 ise kabul edilebilir derecede güvenilir

0.7 ≤ α < 0.9 ise iyi derecede güvenilir

0.9 ≤ α ise çok güvenilir, şeklinde yorumlanır.

Geçerlilik ise ölçülmek istenilen özelliğin, kullandığınız ölçekle doğru ölçüle bilirliğidir. Ölçek güvenilir olsa bile istediğiniz özelliği doğru ölçmeyebilir. Ölçeğin geçerliliği de tıpkı, güvenilirliği gibi oransal olarak yorumlanır. Geçerlilik de güvenilirlik gibi alt gruplara ayrılarak incelenmektedir.

Örnek: Hemşirelerin tükenmişlik düzeyleri ile ilgili bir araştırmada kullanılan bir ölçeğin güvenirliliğin ölçülmesi amacı ile IBM SPSS’ te izlenecek yol aşağıdaki şekildedir:

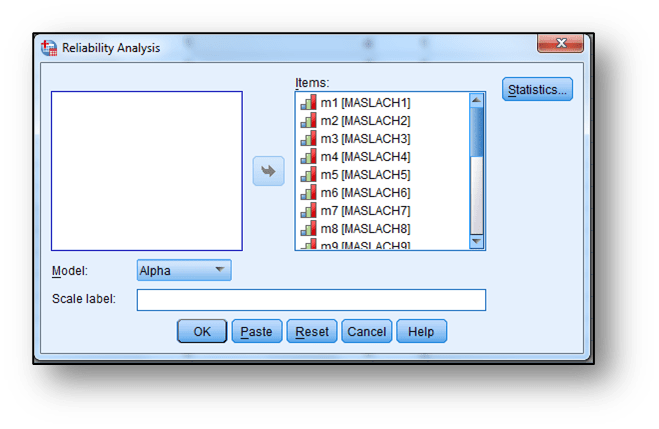
Analyze / Scale / Reliability Analysis

Sekmeleri tıklanır, açılan ekranda “Items” bölümüne güvenilirliği incelenecek olan değişkenler aktarılır ve “OK” butonuna tıklanarak Cronbach α değeri elde edilir.

Analiz sonucu IBM SPSS çıktı ekranında elde edilen tablolar aşağıda yer almaktadır:

Case Processing Summary
		N	%
Cases	Valid	1237	100,0
	Excludeda	0	,0
	Total	1237	100,0
a. Listwise deletion based on all variables in the procedure.

Reliability Statistics
Cronbach’s Alpha	N of Items
,802	22

Tablo ölçeğin madde sayısı ile birlikte cronbach’s alpha değerini de vermektedir. Bu örnekte teste tabi tutulan 22 ölçek maddesi vardır ve elde edilen Cronbach α değeri 0.802’dir. Bu değer bu ölçeğin iyi derecede güvenilir bir ölçek olduğunu göstermektedir.

📚 Kaynakça

Aksaraylı, M. (2020), “BİLGİSAYAR DESTEKLİ VERİ ANALİZİ ve IBM SPSS DERS NOTLARI“, Dokuz Eylül Üniversitesi, İzmir

Özdamar K. (1999). Paket Programlarla İstatistiksel Veri Analizi-1. Eskişehir: Kaan Kitapevi.

Yalcinkaya A.E. (2008). Kategorik Veri Analizinin İstatistiksel Veri Analizi İçerisindeki Yeri Ve Önemi (İzmir : Dokuz Eylül Üniversitesi, Sosyal Bilimler Enstitüsü, Yüksek Lisans Tezi,2008),46-224.

---

🖋 Dr. Ayşem Ece Yalçınkaya – Veri Analizi ve Yönetim Sistemleri Eğitmeni, Denetçi ve Süreç Mimarı

📌 www.aysemece.com | 📧 iletisim: aysemece@gmail.com