Regresyon analizi, bağımlı değişken ile bağımsız değişkenler arasındaki ilişkileri ölçmek ve tahmin etmek için kullanılan bir istatistiksel yöntemdir. Bu analiz, özellikle iki veya daha fazla nicel değişken arasındaki ilişkileri anlamak için tercih edilir ve doğrusal ya da doğrusal olmayan modellerle gerçekleştirilebilir. Regresyon analizi, birçok farklı alanda kullanılabilen güçlü bir istatistiksel araçtır.
İkiden fazla faktör tarafından etkilenen olaylarda, bağımlı değişkendeki değişimi tek bir bağımsız değişkenle ile açıklamak yerine modele birden çok bağımsız değişken eklenmektedir.
Bir bağımlı ve çok sayıda bağımsız değişkene sahip regresyon modellerine çoklu regresyon modeli denir. Örneğin, bir şirketin karı (bağımlı değişken), hammadde fiyatları, işçilik ücretleri, ülkenin genel iktisadi koşulları, gelir dağılımı, tamamlayıcı malların fiyatları, rakip malların fiyatları, denetim maliyetleri ve müşteri özel istekleri gibi çok sayıda bağımsız değişkenden etkilenebilir. Bu durumda çoklu regresyon modeli kullanmak en iyi yöntem olacaktır.
Çoklu regresyonda ana kütle regresyon modeli, örnek alınarak tahmin edilmektedir.
Ana kütle çoklu regresyon modeli aşağıdaki formülle ifade edilmektedir:
ϒi = β1 + β2X2 + β3X3 + β4X4 +….+ βkXk +ϵi
ϒi : Bağımlı değişken
β1 : Sabit katsayıyı
β2, β3, β4, … βk :Bağımsız değişkenlerin katsayılarını ifade eder.
Basit regresyonda olduğu gibi çoklu regresyonda da hata terimi ile ilgili temel varsayımlar aşağıdaki gibi sıralanır :
- Normallik varsayımı
- Sıfır ortalama varsayımı
- Otokorelasyon olmaması varsayımı
- Sabit varyans varsayımı
- Bağımsız değişkenin tesadüfi değişken olmaması varsayımı
- Çoklu doğrusal bağlılık olmaması
- Örnek birim sayısının tahmin edilecek parametre sayısından büyük olması
Örnek olarak, tüketim gelir ilişkisinin incelenmesinde, hane halkının kişi sayısı da bağımsız değişken olarak modele eklendiğinde çoklu regresyon modeli tercih edilmelidir. Bu tahmin modeli için IBM SPSS menüsünde seçimler:
Analyze / Regression / Linear —-> Sekmeleri tıklanarak basit regresyondaki adımlar aynı şekilde izlenir. Burada “Independent(s)” alanına birden fazla bağımsız değişken aktarılır ve “OK” e tıklanır.
Output ekranına yansıyan sonuç tabloları sıralaması, basit regresyon modeli tahmin sonuçları ile aynıdır. İlk tablo değişkenlere ait ortalama ve standart sapma değerlerini vermektedir ve hane halkı kişi sayısının ortalaması 2.85, standart sapması 1.098’dur.
| Descriptive Statistics | |||
| Mean | Std. Deviation | N | |
| tüketim | 11,15 | 2,346 | 20 |
| gelir | 26,95 | 6,817 | 20 |
| Kişi sayısı | 2,85 | 1,089 | 20 |
Değişkenler arasındaki ilişkinin incelenmesi için korelasyon katsayısını veren ikinci sonuç tablosu, hane halkı kişi sayısı ile tüketim arasındaki korelasyon katsayısı 0.689 olduğu görülmektedir. Bu katsayıya ait p değeri 0.000’dir. Bu durumda tüketim ile hane halkı kişi sayısı arasında pozitif kuvvetli bir ilişki vardır. Hane halkı kişi sayısı ile gelir arasındaki korelasyon katsayısı 0.545 olduğu görülmektedir. Bu katsayıya ait p değeri 0.007’dir. Bu durumda gelir ile hane halkı kişi sayısı arasında pozitif orta düzeyde bir ilişki vardır.
| Correlations | ||||
| Tuketim | Gelir | Kişi sayısı | ||
| Pearson Correlation | tuketım | 1,000 | ||
| gelır | ,853 | 1,000 | ||
| kısısayısı | ,689 | ,545 | 1,000 | |
| Sig. (1-tailed) | tuketım | . | ||
| gelır | ,000 | . | ||
| kısısayısı | ,000 | ,007 | . | |
| n | tuketım | 20 | 20 | 20 |
| gelır | 20 | 20 | 20 | |
| kısısayısı | 20 | 20 | 20 | |
Sonuç tablolarının üçüncüsü, değişkenlerin modele eklenmesi sırasında kullanılan metodun bilgisini vermektedir. Bu örnekte “Enter” metodu kullanılmıştır.
| Variables Entered/Removeda | |||
| Model | Variables Entered | Variables Removed | Method |
| 1 | kısısayısı, gelırb | . | Enter |
| a. Dependent Variable: tuketım | |||
| b. All requested variables entered. | |||
Bir sonraki çıktı tablosu, model için özet istatistikleri içermektedir. Tüketiminin, hane halkı kişi sayısı ve gelir ile açıklandığı çoklu doğrusal regresyon modelinin belirlilik katsayısı (R2) 0.799’dur.
Tüketimin sadece gelir ile açıklandığı basit regresyon modelinde belirlilik katsayısı 0.728 olarak elde edilmiştir.
Modele eklenen her değişken, açıklamayı arttıracağından çoklu doğrusal regresyon modelinin belirlilik katsayısında azda olsa bir artış söz konusudur.
| Model Summaryb | ||||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate |
| 1 | ,894a | ,799 | ,775 | 1,112 |
| a. Predictors: (Constant), kısısayısı, gelır | ||||
| b. Dependent Variable: tuketım | ||||
Çıktı tablolarından Anova ile modelin geçerli olup olmadığı test edilir.
Model test edilirken p değerine bakılır. Bu değer 0.05’ten küçük ise modelin geçerli bir model olduğu anlaşılır. Bu örnekte p = 0.000 olarak bulunmuştur. Bu nedenle analiz sonucunda elde edilecek modelin geçerli bir model olduğu görülmektedir.
| ANOVAa | ||||||
| Model | Sum of Squares | df | Mean Square | F | Sig. | |
| 1 | Regression | 83,544 | 2 | 41,772 | 33,806 | ,000b |
| Residual | 21,006 | 17 | 1,236 | |||
| Total | 104,550 | 19 | ||||
| a. Dependent Variable: tuketım | ||||||
| b. Predictors: (Constant), kısısayısı, gelır | ||||||
Coefficient tablosu ile modelin parametre tahminleri yapılır. Bu sonuçlara göre, modelde yer alan hem eğim parametreleri hem de sabit parametre istatistiksel olarak anlamlıdır. Üç parametre için de p değerleri 0.05’ten küçüktür.
| Coefficientsa | ||||||
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | ||
| B | Std. Error | Beta | ||||
| 1 | (Constant) | 2,894 | 1,048 | 2,761 | ,013 | |
| gelır | ,234 | ,045 | ,679 | 5,240 | ,000 | |
| kısısayısı | ,687 | ,279 | ,319 | 2,461 | ,025 | |
| a. Dependent Variable: tuketım | ||||||
Elde edilen sonuçlar temel alınarak çoklu doğrusal regresyon modeli şu şekilde yazılabilir.
ϒi = β1 + β2X2 + β3X3 + β4X4 +….+ βkXk +ϵi
ϒi = 2.894 + 0.234 X2 + 0.687 X3
Tüketim = 2.894 + 0.234 (Gelir) + 0.687 (Hanehalkı)
Bu durumda; gelirdeki bir birimlik artış, tüketimi 0.234 birim; hane halkı sayısındaki bir birimlik artış, tüketimi 0.687 birim artırmaktadır.
| Residuals Statisticsa | |||||
| Minimum | Maximum | Mean | Std. Deviation | N | |
| Predicted Value | 7,55 | 16,14 | 11,15 | 2,097 | 20 |
| Residual | -2,578 | 2,282 | ,000 | 1,051 | 20 |
| Std. Predicted Value | -1,715 | 2,382 | ,000 | 1,000 | 20 |
| Std. Residual | -2,319 | 2,053 | ,000 | ,946 | 20 |
| a. Dependent Variable: tuketım | |||||
Çoklu regresyonda da, basit regresyonda olduğu gibi analiz sonunda artıklar ile ilgili istenen bilgilerin bulunduğu tablo ile grafiksel gösterimler de elde edilmektedir.
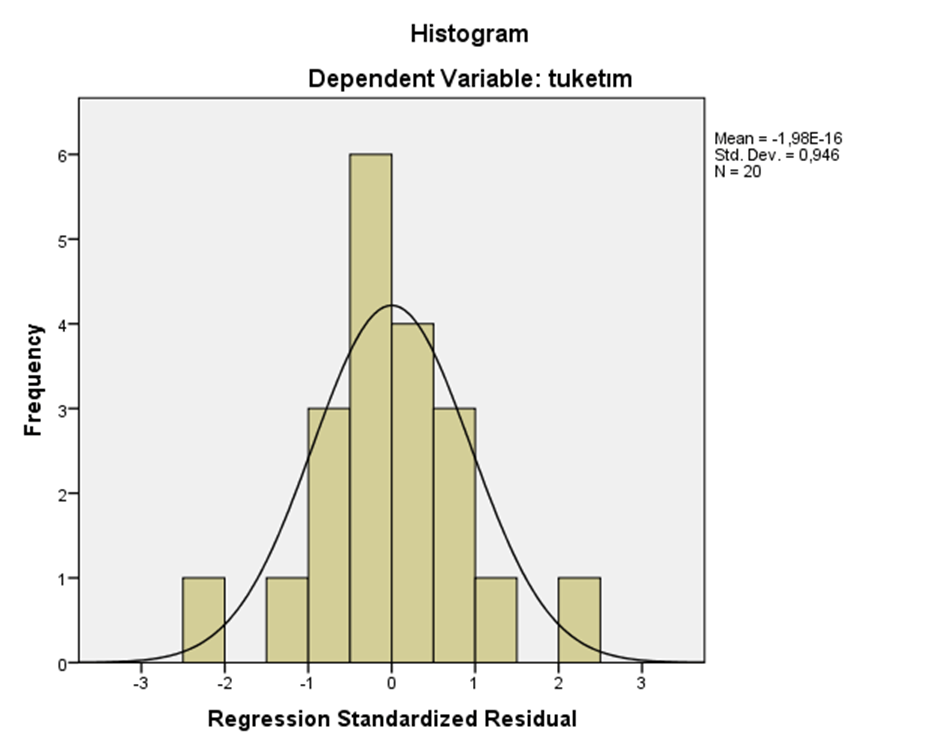
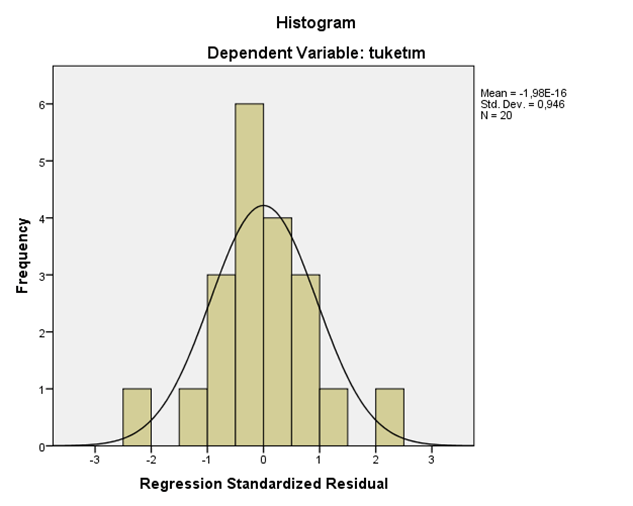
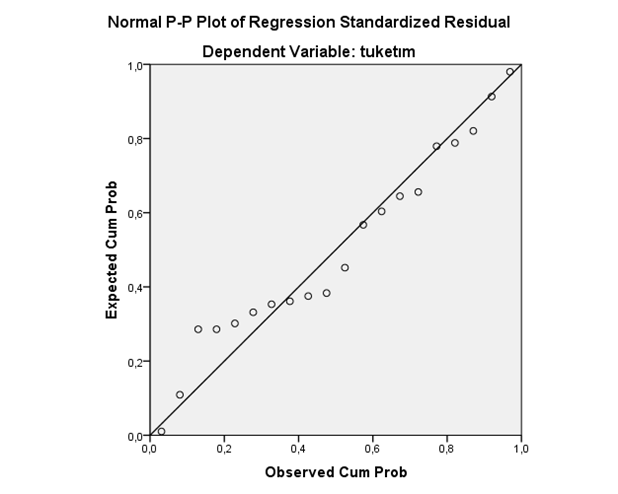
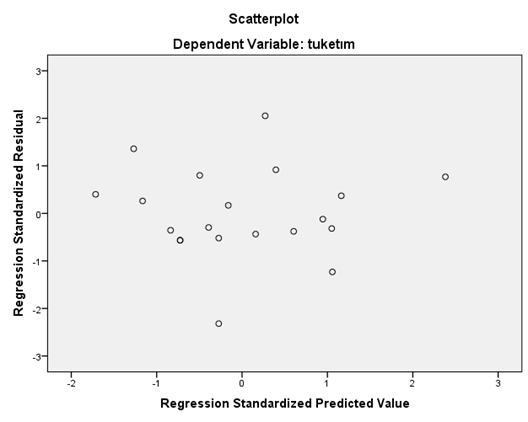
Bir sonraki yazıda Regresyonda Model Seçimi (Stepwise Regresyon Yöntemi) ele alınacaktır.
Size fayda sağlayacak online kaynaklar:
https://www.nobelyayin.com/en/ibm-spss-ile-istatistiksel-veri-analizi-19831.html
https://www.ibm.com/docs/tr/spss-statistics
🖋 Dr. Ayşem Ece Yalçınkaya – Veri Analizi ve Yönetim Sistemleri Eğitmeni, Denetçi ve Süreç Mimarı


