Kesikli Şans değişkenlerinin olasılık dağılımlarından en önemlilerinden biri olarak ifade edilse de Bu dağılışta n sürekli ve x kesikli değerler alabiliceğinden hem sürekli hem de kesikli dağılışlarla ilgilidir.
Binom dağılımının limitidir ve ek olarak üstel(exponential) dağılışa temel oluşturur.
Günlük hayat ve uygulamada çok sayıda kullanımı vardır. Belirli bir alan içerisinde rasgele dağılan veya belirli bir zaman içinde rasgele gözlenen olayların olasılıklarının hesaplanabilmesi için kullanışlı bir modeldir.
Belirli bir zaman ya da alan birimi içinde belirlenmiş sayıda olayın gerçekleşme olasılığını hesaplamak için kullanırız. Belirli bir aralıkta ilgilenilen olayın gerçekleşme olasılığının çok küçük olduğu durumlarda kullanılır.
Örnekler
- Bir bankada çek işlemleri sıraya giren kişilerin sayısı,
- Bir çalışanın bir çalışma yılı içerisinde ortalama 10 gün hasta geçirme olasılığı,
- Uçak şirketinin 6 aylık süreçte 2 defa rötar yapma olasılığı,
- Bir işletmenin aylık hatalı ürün sayısının hedeflenen sayıyı geçmesi olasılığı,
- Bir mahallede bir aylık süre içerisinde meydana gelen hırsızlık sayısı,
- İstanbulda 100 metrekareye düşen birey sayısı,
- Marmara bölgesinde 6 aylık bir periyotta 4.0 şiddetinden büyük gerçekleşen depremlerin sayısı.
Bunları hesaplamak istersek poisson dağılımından fayda sağlanır. En önemli noktanın, olması beklenen olayların nadir gözlemlenen olaylar olduğu başka bir ifade ile gerçekleşme olasılığının çok küçük olduğu görülmektedir.
X şans değişkeni n ve p parametreli Binom Dağılımı göstermek üzere, n deneme sayısının büyük olduğu ayrıca p başarı olasılığının küçük olduğu durumlarda ( tercihen np ≤ 5 ) , x şans değişkeni ile ilgili olasılık hesaplamalarında kolaylık sağlaması açısından Binom Dağılımı yerine Poisson Dağılımı kullanılır. Binoma yakın sonuçlar verir.
Her iki dağılımın beklenen değeri(ortalaması) birbirine eşitlenir ve buradan λ’nın tahmini elde edilir.
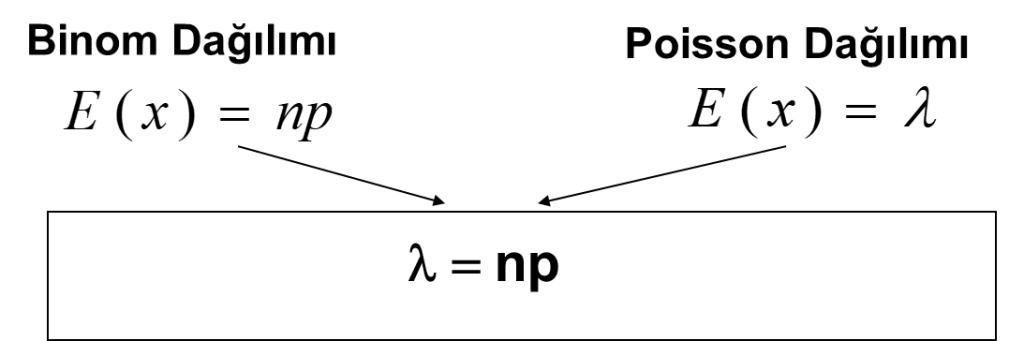
Bu dağılışın şekli λ’ya bağlıdır. λ büyüdükçe dağılım mod’a sahiptir ve aralıklar genişler, simetrik hale dönüşür.

Özellikleri:
Poisson dağılımı, aşağıdaki koşulları sağlayan rastgele bir değişken x’in ayrık bir olasılık dağılımıdır.
- Deney, belirli bir aralıkta bir olayın kaç kez meydana geldiğine, sayma esasına dayanır. Bu aralık; zaman, alan veya hacim aralığı olabilir.
- Olayın meydana gelme olasılığı her aralık için aynıdır. Belirlenen periyotta meydana gelen ortalama olay sayısı sabittir.
- Ortaya çıkan olay sayısı ile periyodun uzunluğu doğru orantılıdır.
- Mümkün olabilecek en küçük zaman aralığında en fazla bir olay gerçekleşebilir.
- Bir olayın bir aralıkta gerçekleşme sayısı bir başka aralıktan tamamen bağımsızdır.
- Olay, bağımsız aralıklarda da gerçekleşse diğer bağdaşmayan aralıklarda da gerçekleşse, tanımlanan aralıkta olayın x defa gerçekleşme olasılığı,
- Beklenen değeri ve varyansı birbirine eşit tek dağılımdır.
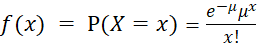
e, doğal logaritmanın tabanı (e = 2.71828…)
μ = E(x) = λ =n.p (populasyon ortalaması)= var(x)
Binom Olasılık Dağılım Fonksiyonundan Poisson Olasılık Dağılım Fonksiyonun türetilmesi:
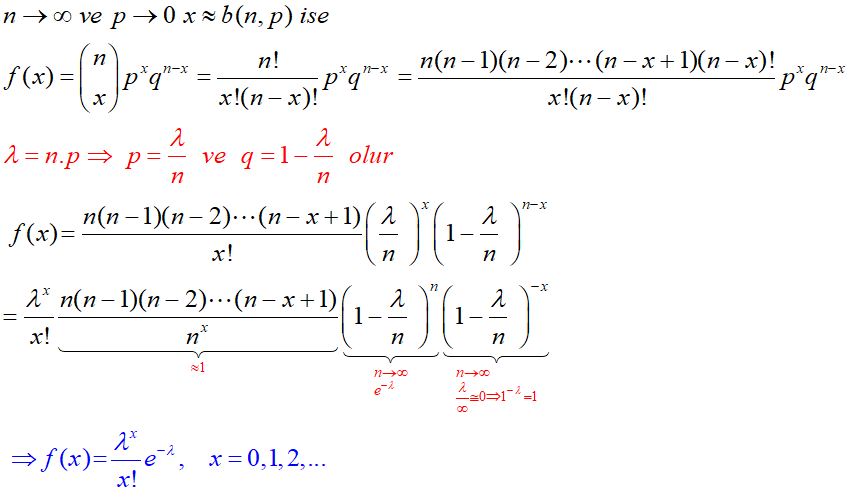
Örnek: Bir sigorta şirketinin müşterilerinin trafik kazası sonucunu hayatını kaybetme olasılığı 0,003’dür. Sigorta şirketinin müşterilerinden 1000 kişilik bir örnek alındığında,
a) 4 müşterinin,
b) En az iki müşterinin trafik kazasında hayatını kaybetme olasılığın hesaplayınız.

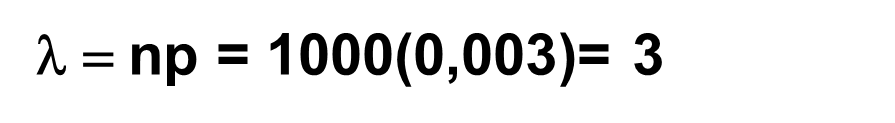


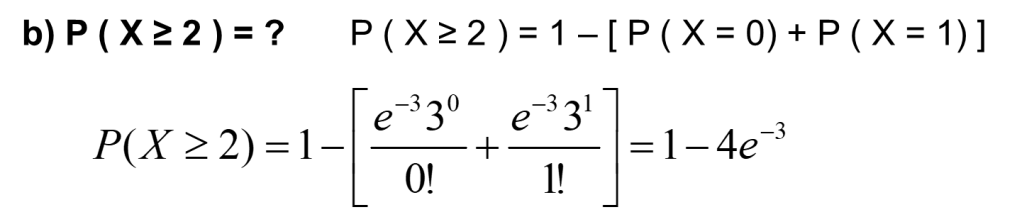
Örnek:
Poisson Regresyon Modeli yakında…
Referans:
Turney, S. (2023, June 21). Poisson Distributions | Definition, Formula & Examples. Scribbr. May 28, 2025, from https://www.scribbr.com/statistics/poisson-distribution/
Aksaraylı, M. (2019). Ders Notları.
🖋 Dr. Ayşem Ece Yalçınkaya – Veri Analizi ve Yönetim Sistemleri Eğitmeni, Denetçi ve Süreç Mimarı