IBM SPSS ile Poisson Regresyon Analizi

“Poisson regresyon, sayımla ifade edilen verilerin analizinde en güçlü araçlardan biridir.”
— Alan Agresti (Kategorik Veri Analizi uzmanı)

Poisson regresyon, bağımlı değişkenin sayma verisi (count data) olduğu durumlarda kullanılan bir regresyon modelidir:

• Olayların sayısının zamanla değiştiği durumlar (örneğin, bir gün içinde açan çiçek sayısı).
• Olayların belirli bir alanda (örneğin, bir kilometrekaredeki trafik kazaları) meydana gelmesi.
• Olayların sayısının, belirli bağımsız değişkenlerle (örneğin, hava durumu, günün saati) ilişkili olduğu durumlar.

Bir çağrı merkezinde çalışanların günlük çözdüğü müşteri şikayeti sayısı (bağımlı değişken), çalışanların deneyim yılı ve eğitim durumu (bağımsız değişkenler) ile ,

Belirli kilometrekarelerdeki trafik kazalarının sayısı (bağımlı değişken), yolun zemin durumu, hava şartları, sürücülerin ehliyete sahip olma yılları, araba türleri, günün saatleri (bağımsız değişken) ile açıklanmak istenebilir.

Poisson Regresyon Denklemi

Poisson regresyonu, bazı varsayımlar gerektirir. Örneğin, olayların bağımsız olması ve ortalama ile varyansın eşit olması gibi. Bağımlı değişkenin Poisson dağılımına sahip olması gerekmektedir. Eğer bu varsayımlar sağlanmıyorsa, modelin geçerliliği sorgulanabilir. Bu durumda, alternatif modeller (örneğin, Negatif Binom Regresyonu) düşünülmelidir.

Veri Hazırlık

Öncelikle veri seti IBM SPSS programına yüklenir veya verileri programa işlenir. Bağımlı değişken sayma verisi / sayım / count tipi (örneğin hasta sayısı, üye sayısı, kaza sayısı gibi pozitif tam sayılar) olmalıdır. Bağımsız değişkenler; sürekli (örneğin saat sayısı) veya kategorik olabilir.

Varsayım Kontrol

Denge (Equidispersion): Ortalama = Varyans mı kontrol edilir. Aykırı değer ya da eksik model yapısı varsa aşırı dağılım (overdispersion) görülebilir.

Gerekirse “scale parameter” olarak Pearson veya deviance seçeneği ile ya da robust covariance ile ayar yapabilir. Aşırı dağılım devam ederse, Negatif binom regresyonu düşünülmelidir.

Önce girilen bağımlı değişkene ait verilerin ortalaması alınır. Bu ortalama değer Analyze -> Nonparametric Tests -> Legacy Dialogs -> 1 Sample K-S sekmesinden açılan “One-Sample Kolmogorov-Smirnov Test” adlı diyalog kutusunun Poisson (G) yeri tıklanarak girilir. Test variable kısmına bağımlı değişken atanır ( scale ölçek) ve çıktı tablosundaki Sig. p değeri, 0.05’ten büyük ise, verimiz Poisson dağılımına sahiptir. Alternatif yol ise “Descriptive Statistics” seçeneği tıklanarak bağımlı değişkene ait Mean ve Variance değerleri tablosu kontrol edilir ve yaklaşık olarak eşit ise veri Poisson dağılımlıdır denilebilir.

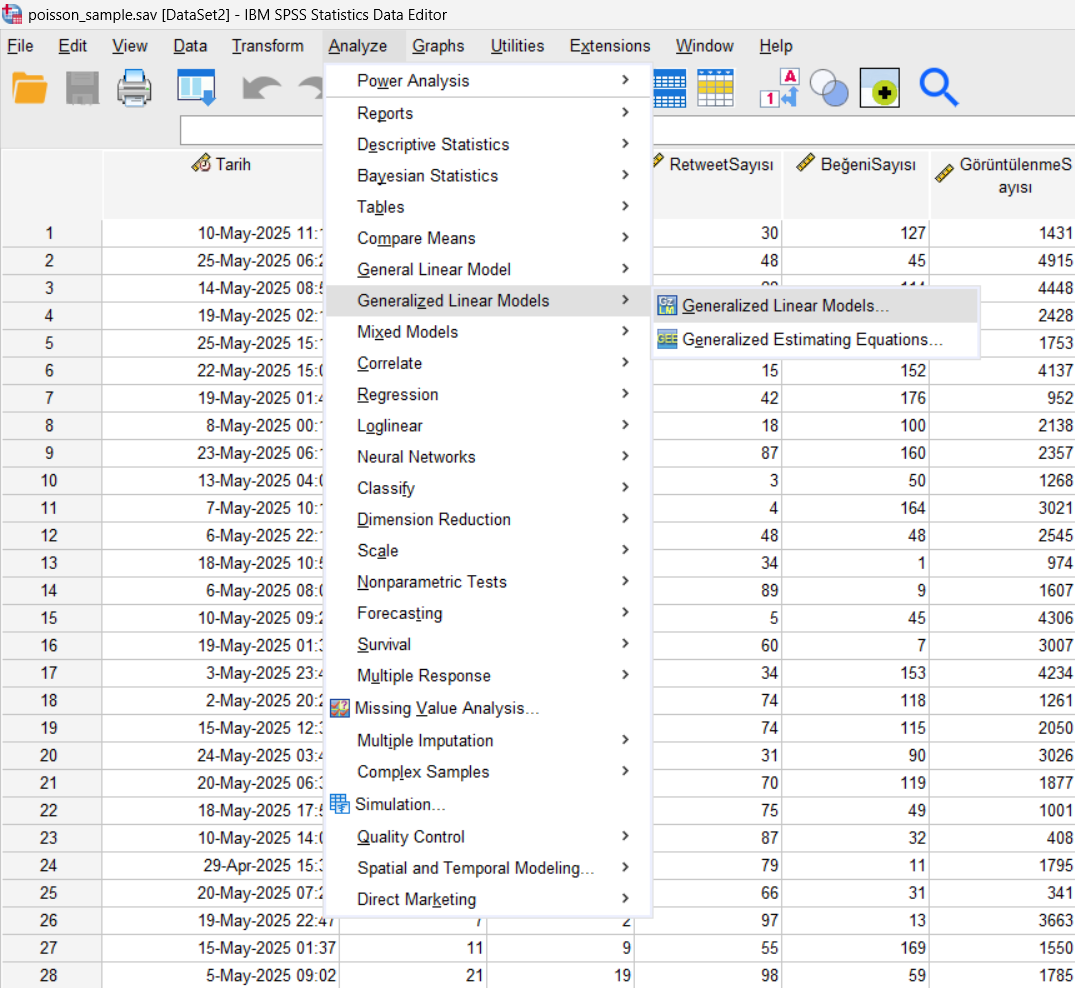
IBM SPSS menü seçimi

SPSS’te: Analyze → Generalized Linear Models → Generalized Linear Models… yolu izlenir. Açılan pencerede “Type of Model” sekmesinden Poisson loglinear’ı seçilir . “Link Function” otomatik olarak Log seçili gelecektir ( değiştirilmemelidir).

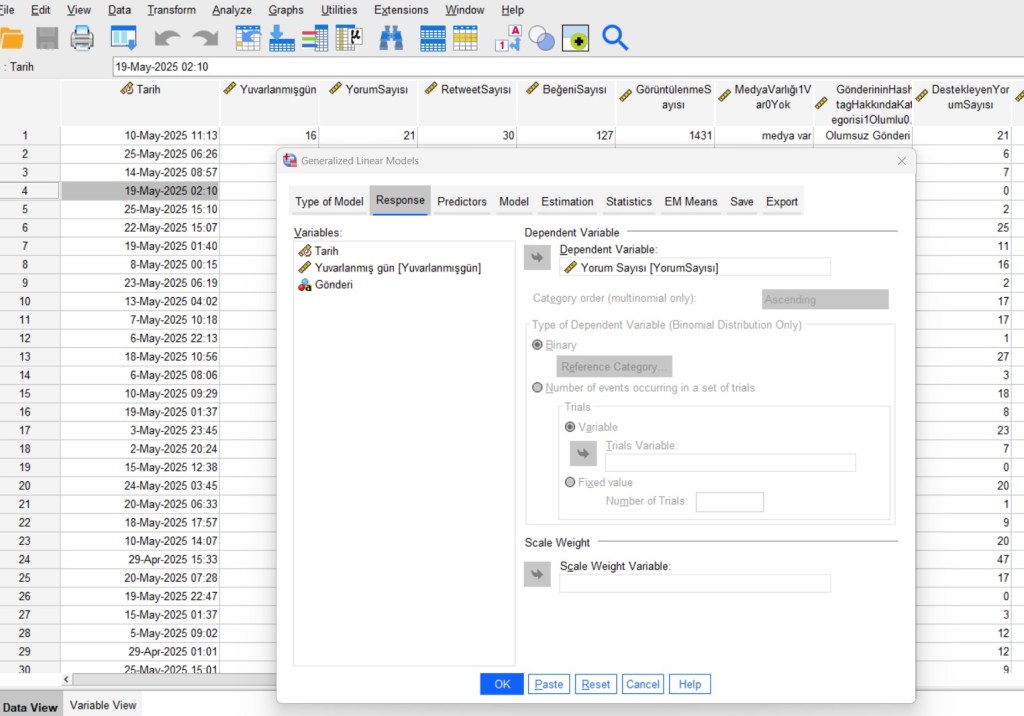
• Response sekmesinde bağımlı değişken,
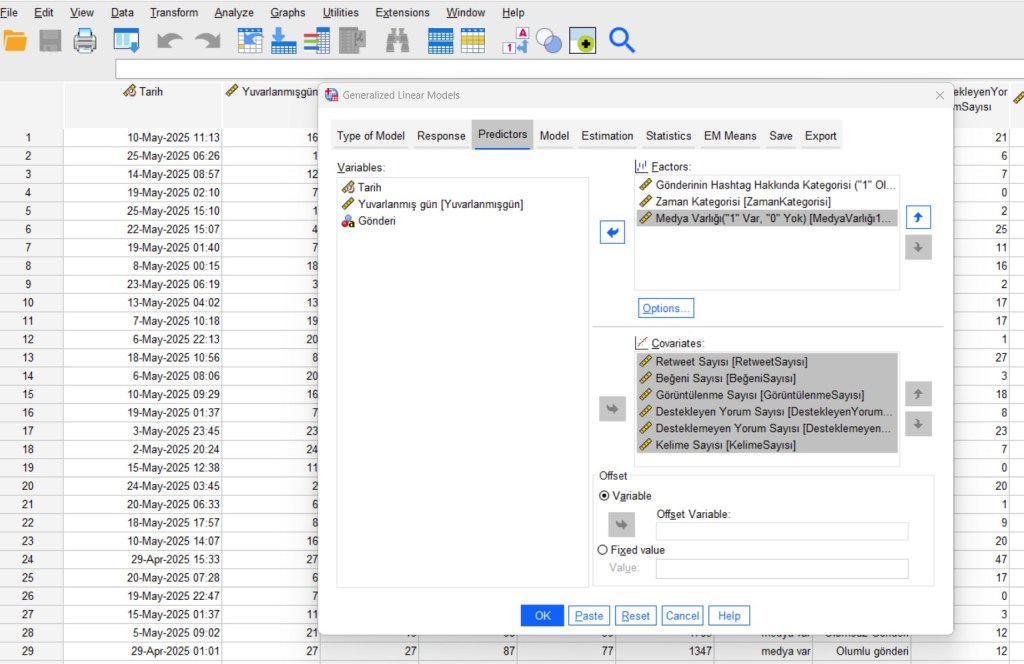
• Predictors sekmesinde kategorik değişkenler “Factors” kutusuna, sürekli değişkenler “Covariates” kutusuna taşınır.
• Model sekmesinde “Main Effects” kuralını seçip, bağımsız değişkenler modele eklenir.
• İsteğe bağlı etkileşim (“Interaction”) veya nested modeller de buradan kurulabilir.
• Estimation sekmesinde varsayılan ayarlar (Deviance veya Pearson) kabul edilir.

• Statistics sekmesinde “Include exponential parameter estimates” seçeneği işaretlerinerek sonuç ekranında Exp(B) (odds ratio benzeri) değerler raporlanır.

Hepsi tamamlandıktan sonra OK sekmesine tıklanır ve Output ekranında sonuçlar elde edilir.

IBM SPSS Çıktı Ekranı (.sav uzantılı):

IBM SPSS çıktılarını anlamak için aşağıdaki tablolar önemlidir:

• Model Information – Modelin log link ve Poisson dağılımlı olduğunu gösterir.
• Case Processing Summary – Ele alınan örnek sayısını verir.
• Goodness of Fit – Pearson Chi-Square ve Deviance istatistiklerine bakılır. Chi-Square / df ≈ 1 olmalı → model uyumu iyi; aşırı veya eksik dağılımdan kaçınılmalıdır. Chi-Square / df = 1 ise overdispersion (aşırı dağılım) olabilir.
• Omnibus Test – Bağımsız değişkenlerin model geneline etkisini test eder. Model genel olarak anlamlı mı?
  p < 0.05 ise modeliniz bağımsız değişkenlerle anlamlı ilişki kuruyor demektir.
• Tests of Model Effects – Her değişkenin tekil anlamlılığını inceler. Her bir bağımsız değişkenin modele katkısı test edilir. p < 0.05 olan değişkenler anlamlıdır.
• Parameter Estimates – B ve Exp(B) değerleri burada görünür. B katsayıları, Exp(B) değerleri (etki oranları) ve anlamlılık testleri verilir. Örneğin Exp(B)=1.20 ise, bağımsız değişkendeki bir birim artışla olay sayısı %20 artar.
  

Menü	Açıklama
Analyze → GLM	Poisson loglinear seçilir
Response	Bağımlı değişken tanımlanır
Predictors	Faktör ve covariate değişkenleri eklenir
Model	Ana etki ya da etkileşim tanımı yapılır
Statistics	Exp(B) sonuçları eklenir
OK	Çıktılar değerlendirilir

SPSS sonuç penceresinde şu tablolar çıkacak:

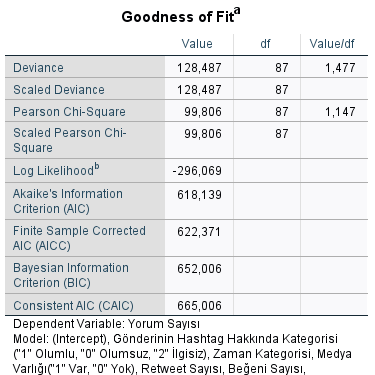
• -2 Log Likelihood: Düşükse daha iyi.
• AIC / BIC: Karşılaştırma yaparken kullanılır (düşükse daha iyi).

Parametre Tahminleri (Coefficients)

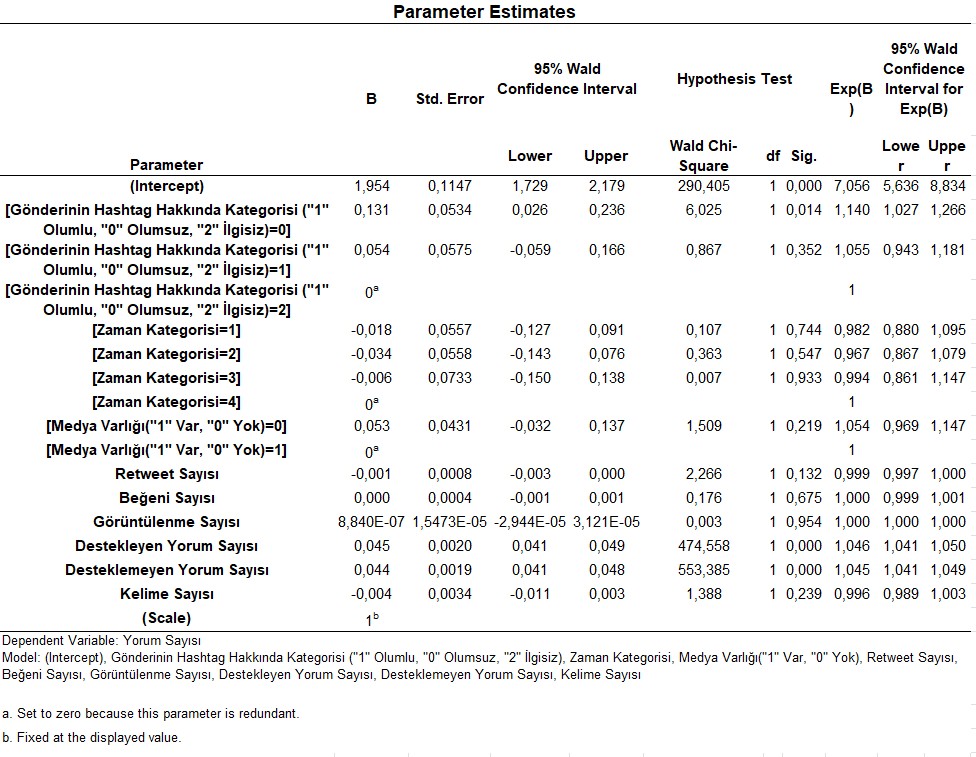
Yorum Örneği: Destekleyen Yorum Sayısı (Exp(B)=1.046): Destekleyen yorum sayısındaki 1 birim artış, genel yorum sayısını  %4,6 artırır (IRR > 1 olduğu için).

Aşırı Yayılım (Overdispersion) Kontrolü

Poisson regresyon, varyans = ortalama varsayar. Eğer varyans > ortalama ise Negatif Binom Regresyon kullanılmalıdır.

Kontrol için:

“Statistics” sekmesinden “Pearson Chi-square” ve “Deviance” değerlerine bakın. Değerler serbestlik derecesine (df) yakınsa model uyumu iyidir. Değerler çok büyükse aşırı yayılım var demektir.

Alternatif: Negatif Binom Regresyon (Overdispersion Varsa)

Eğer aşırı yayılım varsa: “Type of Model” sekmesinde “Negative binomial with log link” seçin. Aynı adımları tekrarlayın.

Özetle:

 Poisson Regresyon: Sayma verileri için kullanılır.
 Exp(B): “Rate Ratio” (IRR) verir. 1’den büyükse risk artar, küçükse azalır.
Aşırı yayılım varsa Negatif Binom kullan…

📚 Kaynakça

• Hilbe, J. M. (2011). Negative binomial regression (2nd ed.). Cambridge University Press. → Poisson ve negatif binom regresyonun teorik altyapısı.
• Dobson, A. J., & Barnett, A. G. (2018). An introduction to generalized linear models (4th ed.). CRC Press. → GLM çerçevesinde Poisson modeli anlatılır.
• IBM Corp. (2022). IBM SPSS Statistics for Windows, Version 28.0 [Software]. Armonk, NY: IBM Corp. → SPSS’in kendisi kaynak olarak gösterilir.
• Garson, G. D. (2012). Generalized linear models: Binary, Poisson, and multinomial regression. Statistical Associates Publishing. → Uygulamalı anlatım ve SPSS üzerinden açıklamalar içerir.
• Long, J. S., & Freese, J. (2006). Regression models for categorical dependent variables using Stata (2nd ed.). Stata Press.

---

🖋 Dr. Ayşem Ece Yalçınkaya – Veri Analizi ve Yönetim Sistemleri Eğitmeni, Denetçi ve Süreç Mimarı

📌 www.aysemece.com | 📧 iletisim: aysemece@gmail.com